Catamorphism as prototype of recursive algorithms
Table of content
WARNING: This is just a informal post on algorithms and most of ideas are only checked on leetcode problems.
Actually I was trying to find some universal methods for solutions on algorithm problems. However, since I only have time to practise on leetcode problems and don't have time to explore in a much broader range like ACM, I hereby only demonstrate my discoveries during solving about 500 problems on leetcode:
For most basic algorithms, no need to master various kinds of tricks and data structures. All these problems can be solved with one simple principal.
You may be suspective. But you can just think that currently, nearly all algorithms of branches and loops are basically equivalent to those of lambda calculus with recursions. Any traditional algorithm which can be finished in finite steps can also be expressed with lambda calculus and recursions. In a nutshell, lambda calculus is turing complete!
The ultimate principal
Wait! Our mission should be positing a uniform principal of problem solving. Why bother wasting time on lambda calculus and recursions? Now let me show you the magic! It can be described informally as:
All problems can be deconstructed by its input, output and side-effect. We can recursively divide the problem until we can solve it trivially. Finally, we merge all recursive solutions and get the global solution.
Actually, there's nothing novel here. This principal is just trying to reintroduce one archaic motto:
All algorithms can be constructed by divide and conquer.
The only difference is that the archaic principal said nothing about what to divide. Although this principal is so simple that it's even hard to be seen as a discovery, to actually use it, it's much much hard and there exists so many pitfalls. Most pitfalls are basically that, most materials and people failed to follow the principal, let alone finding tricks of it. Here I only enumerate some of crux tricks (someday I may write a systemaic book on this).
Tricks
Recursion as loops
All recursions can be converted to equivalent version of loops with extra data structure(such as stack). In fact, all stack based compilers do this for you automatically.
- show one perticular example
Not only input, but also output!
One common misunderstanding is problems can only be divided by input. In practice, dividing output is quite useful and ubiquitous. Whenever you have difficulty dividing on input, just try output!
All information (data) representing part of the problem can be divided. Although different dividing startegies can lead to different complexities.
Recursion on side effect
Many people insist that many problems can not be solve by divide and conquer as the dividing is not local and cannot be merged into the global solution. However, they all ignored some very critical aspect: the side-effect of functions (algorithms).
In theory, side-effect should be anything that can influence referential transparency. The most interesting fact is that, if you think carefully, effects can be classified into compile-time and run-time.
Run-time effect: extra information
For a problem, the result of our recursion is not simply returning a local solution in most scenarios. I find that we usually need additional recursive information. This is a bit abstract, so let me give you an example, using the sliding window that we often see:
Sliding windows are typically described by divide and conquer: for an input list, decompose it into a list consisting of the last element and all the previous elements. Assuming that I have obtained the solution of all the previous elements (except the last element) through recursion, then we will find that the solution of the first half alone is not enough to support us to get a new solution after incorporating the last element. So we can simply include an additional information, that is, assume that the recursion of the first half can return us an additional information, this additional information contains some information about the sequence adjacent to the last element (in fact, this sequence is what many people call a sliding window). Using this additional information, we find that we can easily update the global solution.
Of course, don't forget that this extra information is recursive. When you require the first half to recursively return the extra information, you must also be able to return the updated extra information (which can be compared to the sliding update of a sliding window). Similarly, if you want to get extra information you want from the upper layer, make sure you can then provide it to the next layer. Although the sliding window is used as an example here, the application scope of the extra information technique is actually much more than that. You will find that monotone stacks, double pointers, prefix sums, etc. are all just special cases of extra information recursion.
Compile-time effect: constraints and proofs
Compile-time effects are rare to mention but also ubiquitous! Besides decomposing on run-time data, you can even divide constraints (proofs)! If you are familiar with dependent type theory, then this is much natural.
Divide one aspect at a time, never both
So you start trying to decompose any data that you think might be useful, but remember never to consider decomposition in multiple dimensions. Instead, decompose the first data (dimension) first, and then consider whether to decompose the second dimension. Otherwise, you will definitely fall into chaos. The most typical example is high-dimensional dynamic optimization. For this kind of problem, you must not rush to decompose it all at once, as you cannot eat hot tofu in a hurry.
Defer dividing
Actually, most problems tagged easy and medium can be divided directly by its input and output. The real hard part is lying under the target to be divided. For instance, in designing the famous quick sort, one learns to rearrange the target array before dividing and recursion. the rearrange can effecttively efface the cost of merging after the recursion which is inevitable in merge sort. Moreover, many hard problems do not directly divide on input or output, nor the given effects. To solve them, one need to design and find a way to effectively construct a new data structure to be divided and recur.
Reuse space
When you try to design additional information again, you may find that the memory used to store the additional information can be reused. In this case, you must try to reuse this memory, which can usually greatly reduce space complexity.
Caching
Don't be afraid of dynamic programming. Just list the recursive formula of recursive divide and conquer, and then use a hashMap to cache the results. If you find that there is no circular dependency in the recursion, then you don't even need a hash. A simple array plus the space reuse mentioned above can solve all dynamic programming.
Pruning
Subproblems can be pruned. Greedy algorithms and early termination with backtracking are both trivially applicable.
Catamorphisms and recursion schemes
F-algebra
- complete formal description after
Basic cata
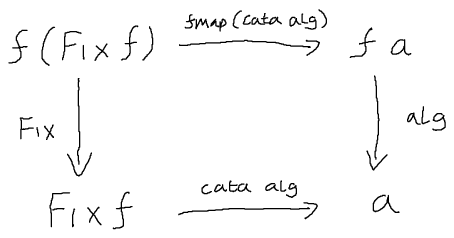
The dividing-and-conquer part can be described by catamorphism. However, in many situations, one need to find a effective target data structure to be divided first which is the real enigma. I shall do more studies on this part.